Policy Gradient
由于我对强化学习一概不知,所以这篇只是将一些重要的强化学习理论进行记录。
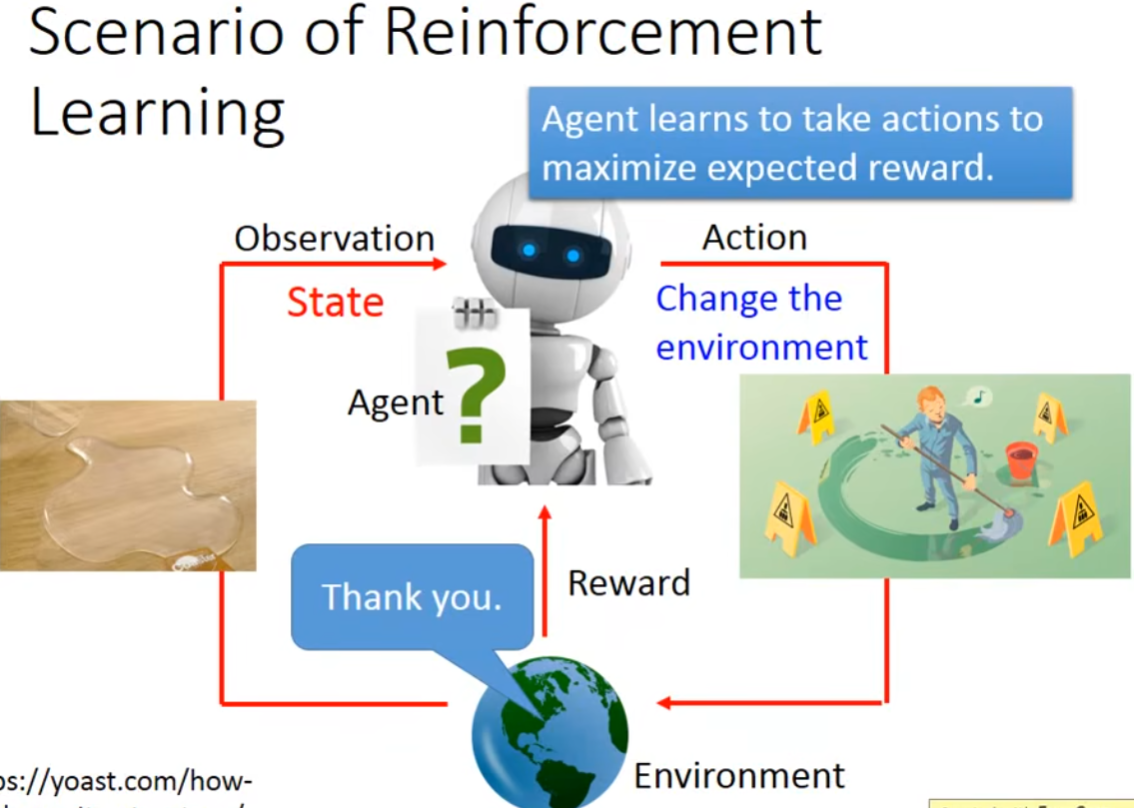
强化学习的场景大致如下,Agent会观察当前环境的状态,并采取对应的行动来改变环境的状态,根据环境的Reward来知道刚才采取的Action是好是坏,最终的目标是要maximize reward。
什么情况下使用强化学习,而非监督学习?
- 首先,很多情况下没有标准答案,人类也无法对当前的state进行评估是好是坏。例如在一个对话场景中,若采用监督学习的方式,那么在Actor返回一句话后,应该有一个标准答案来评判这句话,但这是不可能的,因为回答的样本空间很多。举一个例子,在对话场景中人类发出"Hello",采用监督学习的方式,那么"Hello"的回答应该是"Hi",但我们都知道不止Hi可以回答,还可以回答"How is it going","Nice to meet you","good".....等等,这时候靠监督学习的方式就很难做到列举所有回答的答案。若采用强化学习的方式,Agent就需要根据人类的反应来自行判断回答的质量,例如最终人类生气了,那么Agent就知道自己的发言不妥当,但具体是对话中的哪一句,还是需要Agent自己去学习。
- 其次,数据是问题,某个方向恰好没有大规模的标注数据,这也许是因为标注成本太高,或者是如上文所述,很难标注出Label。那就需要强化学习来让Agent自己学习。
- 监督学习和强化学习也不是二选一,事实上如今大多数的chatbot or Agent都会结合使用。如AlphaGo就会现在标注数据的棋盘上进行监督学习,等到满足一定性能后,才开始进行强化学习。
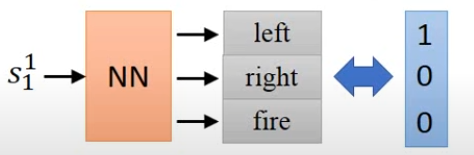
Agent总体可以用一个神经网络表示,输入是当前环境的state,最终的输出是各个action的softmax,然后根据该概率stochastically去采取行动。由于是随机地行动,那么概率越大的行动只是代表被采纳的可能性更大,而非一定采用。可以看到这很像一个分类问题。
那么我们如何判定一个Agent的好坏?就让Agent实际地去跑一趟,得到最终的reward,reward越大越好。我们用\(\pi_{\theta}(s)\)来代表一个Agent,s代表输入的state,\(\theta\)代表Agent的参数。就如上所说,由于同一参数的Agent最终对于同一个state所采取的行动也可能不同,对应的reward也会不同,所以我们要maximize reward的期望值。
我们将一次episode用一个序列\(\tau\)表示: \[ \tau = (s_1,a_1,r_1,s_2,a_2,r_2,...,s_n,a_n,r_n) \] 得到的reward R(\(\tau\))等于: \[ R(\tau) = \sum_{i=1}^n r_i \] 对全部episode求reward期望,得到该Agent的reward期望: \[ \bar{R_{\theta}} = \sum_{\tau}R(\tau)P(\tau|\theta) \] 于是我们的目标是找到一组参数\(\theta\)能让该Agent的reward期望最大化。 \[ \theta^* = \mathop{\arg\max}\limits_{\theta} \bar{R_\theta} \]
我们可以用梯度上升法来找到最大reward对应的\(\theta\)。 \[ \theta^n = \theta^{n-1} + \eta \nabla \bar{R_\theta} \] 即 \[ \nabla\bar{R_{\theta}} = \sum_{\tau}R(\tau) \nabla P(\tau|\theta) \] 所以R(\(\tau\))可以不可微,也可以不知道式子,只需要数值结果。比如一局游戏的Agent,得到的reward就是输赢,具体过程不重要。对于这一步中转换为log的形式,一个合理的解释是除以概率\(P(\tau|\theta)\)可以起到Normalization的作用,不会让Agent偏好于reward低但频率高的Action。 \[ \nabla\bar{R_{\theta}} = \sum_{\tau}R(\tau) \nabla P(\tau|\theta) = \sum_{\tau}R(\tau)P(\tau|\theta) \frac{\nabla P(\tau|\theta)}{P(\tau|\theta)} = \sum_{\tau}R(\tau) P(\tau|\theta)\nabla logP(\tau|\theta) \] 对于\(R(\tau)P(\tau|\theta)\),我们转换为sampling形式,也就是在该参数下进行n个episode,计算对应的reward,最后取平均。 \[ \nabla\bar{R_{\theta}} ≈ \frac{1}{N} \sum_{n=1}^NR(\tau ^n) \nabla logP(\tau^n|\theta) \] 之后计算\(logP(\tau^n|\theta)\) \[ \begin{align} P(\tau|\theta) = P(s_1)P(a_1|s_1,\theta)P(r_1,s_2)P(a_2|s_2,\theta)P(r_2,s_3)P(a_3|s_3,\theta).... \\ = P(s_1)\prod_{t=1}^Tp(a_t|s_t,\theta)p(r_{t},s_{t+1}|s_t,a_t)\hspace{5.6cm} \\ = logP(s_1)+\sum_{t=1}^Tp(a_t|s_t,\theta)+p(r_{t},s_{t+1}|s_t,a_t) \hspace{3.65cm} \end{align} \]
\(\nabla logP(\tau^n|\theta)\)只与\(\theta\)相关,所以可以删掉无关的项。 \[ \nabla logP(\tau^n|\theta) = \sum_{t=1}^T \nabla log\ p(a_t|s_t,\theta) \] 最终得到Policy Gradient:
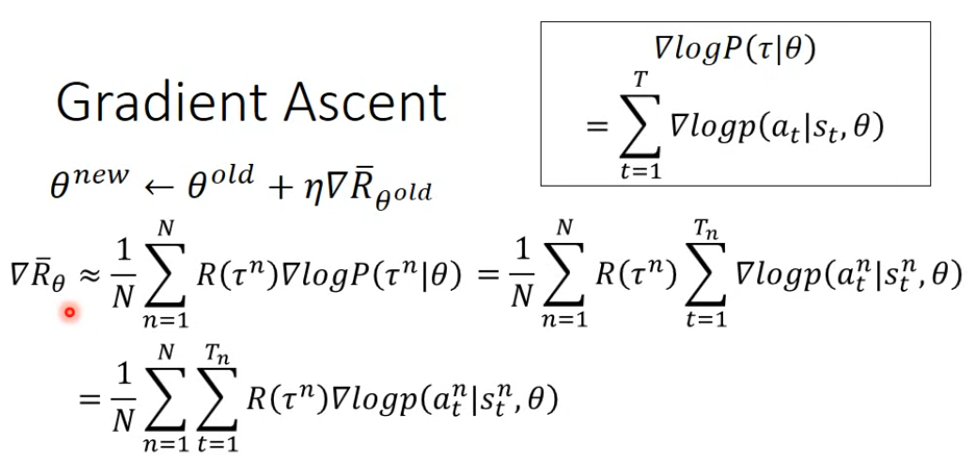
解读最终的式子,首先,我们需要让episode t中能够得到positive行动的概率\(p(a_t^n|s_t^n,\theta)\)的概率大,negative的概率小。然后我们求得整个episode的reward,让其最大,最终目标是让整个trajectory的reward最大。因此我们并非是要求局部最优,而是最全局最优。
举一个例子,吃饭的时候我们一直在吃,每吃一口得到的满足感会+1,但你也可以选择饿5个时间步的肚子,然后狼吞虎咽,得到10的满足感。如果我们是追求局部最优,那么就会一直吃饭,因为只有吃饭才会得到reward,但显然这不是全局最优解。
还有一种可能性,也就是某些Action没有被sample到,而其恰恰是reward比较大的,那么在经过gradient ascent后,其余的低reward的Action概率会增加,这导致reward大但是没见到or少见的Action概率在不断降低。所以我们要设一个baseline,最直接方法就是让\(R(\tau^n)- b\),让reward有正有负,保证Agent会在baseline之上,可以取\(b = E(R(\tau))\),实际上bias的确定也非常复杂。
Critic是帮助Agent评估当前State的,可以合并在一起训练。比如在RL在赛车游戏中,Critic观察到当前的道路比较平坦,很适合加速,那么他会提供一个比较高的reward期望告诉Agent,来让Agent采取加速的行动。
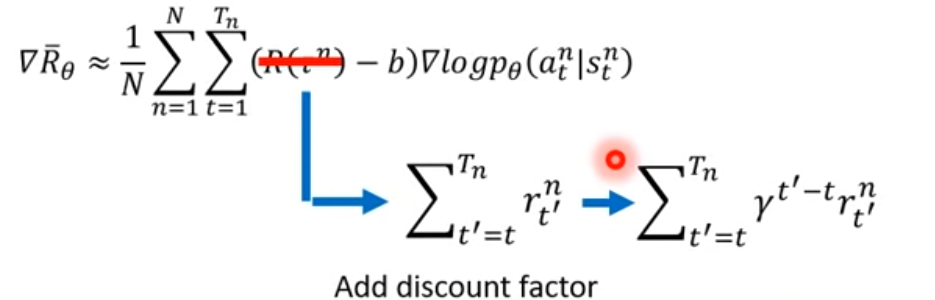
此时的Policy Gradient还有优化的空间,理想状态下,不同的action应该有不同的weight,因为reward的值大,不代表你的每一个时间步\((a_t^n|s_t^n,\theta)\)都是对的,通俗地讲,每一个时间步的Action都会产生对后续的Action的蝴蝶效应。而此时的Policy Gradient对没有把reward的粒度分到action,而是分到了一次episode \(\tau\)中,让他都乘以\(R(\tau^t)\)。所以我们需要给每一个时间步加上一个权重,来表示这个Action对后续的影响。
<img src="../images/image-20240415003057746.png"> 以这张图为例子,除了第一步面对状态\(s_a\)所采取的行动有差异,其他的都一样,但最终得到reward不一样。我们可以认为行动\(a_2\)对后续的\(a_3\)造成了-2的reward,所以是一个不好的行动。直觉上,一个Action对越往后的Action影响应该会越小,就像注意力机制、RNN的长距离依赖,所以还需要做一步discount,在后续的reward总和前乘上一个小于1的\(\gamma\)。最终时间步项所乘上的这一项可以称为Advantage Function,一般由Critic模型生成。
PPO
先知道一个概念,On-Policy直接使用当前策略模型\(\pi_\theta\)与环境交互采样得到样本,使用这些样本计算Policy Gradient,即期望项内\(\pi_\theta\)的样本,这种方式下,更新时使用的数据是由当前策略产生的,因此称为On-Policy。On-Policy的代表算法有REINFORCE、A2C、PPO等。优点是简单、收敛性较好,缺点是样本利用效率低、探索性差。而Off-Policy使用一个贪婪或旧的行为策略\(\mu\)与环境交互采样得到样本,使用这些样本,通过Importance Sampling的方式计算用于优化目标策略\(\pi_\theta\)的Policy Gradient,这种方式下,用于优化的数据不是由目标\(\pi_\theta\)产生,因此称为Off-Policy。
所以最主要的区别就是,On-Policy策略,Agent使用当前参数环境交互,然后计算Policy Gradient,更新参数,之后就使用新的参数\(\theta^{n+1}\)来与环境交互。而Off-Policy则不是使用当前的参数\(\theta^n\)采样。On-Policy策略下,采样占据了非常长的时间,因为要采样一次更新一次。而Off-Policy则用\(\theta'\)来采样一批数据,重复使用这一批数据来更新多次Agent参数。
关于Importance Sampling,假设我们现在没办法从某个分布为p的Generator中采样,只能从某个分布为q的Generator中采样。本来如果要计算\(E_{x\sim p}(f(x))\),我们可以从p中多次采样,然后取平均值来近似期望。但现在只能从q中采样,我们可以把\(f(x)\)的值乘上一个Weight,\(Weight = \frac{p(x)}{q(x)}\)。q和p的分布越接近越好,否则方差差异过大,推导直接套用连续数学期望的积分定义,所以sampling次数太少,会导致两者的期望不同。
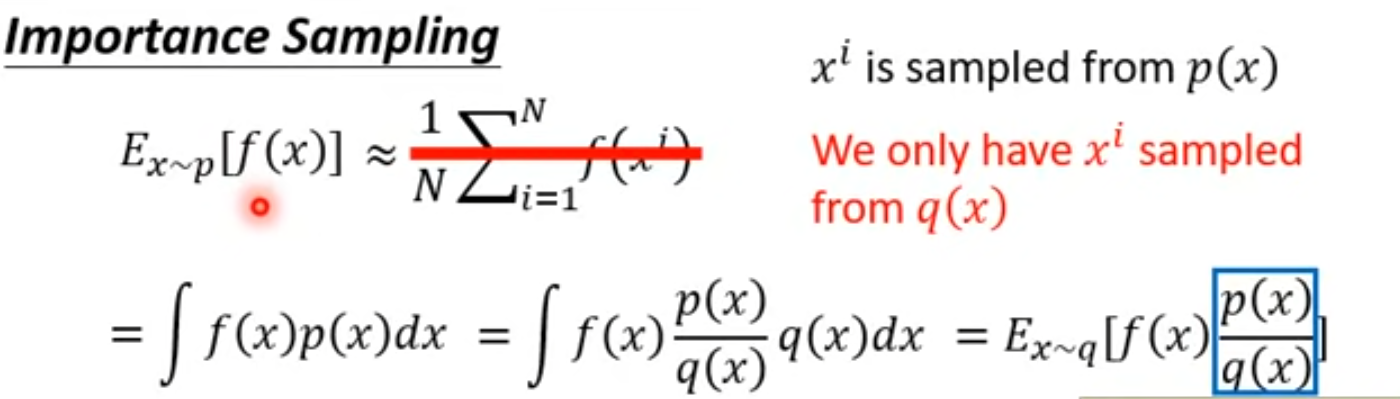

将该结论应用于Off-Policy上。在之前提到过,理想状态下,不同的action应该有不同的weight,因为reward的值大,不代表你的每一个时间步\((a_t^n|s_t^n,\theta)\)都是对的。而此时Critic评估的就不是当前\(\theta\)下某个Action对后续的影响,而是\(\theta'\)对后续的影响。下面用到了一个数学公式,还原出没有做nabla运算下的原式\(J(\theta)\),由于我们做的是梯度上升法,要让原式的值最大,所以最终转换成对\(J(\theta)\)求最大值的问题,这就是Judge Function。


接下来进入PPO,经过上面的讲述,我们知道\(\theta,\theta'\)的分布不能差太多,而PPO就是来解决这个问题。对于描述两个分布之间的差异,我们很自然的就想到KL散度,也称相对熵。 \[ D_{KL}(P \| Q) = \sum_{i} P(i)logP(i) - P(i)logQ(i) =\sum_{i} P(i) \log\left(\frac{P(i)}{Q(i)}\right) \] 其中P为真实分布,KL散度有非负性,两个分布越接近,KL散度越接近0,当前仅当二者相等时为0。
下面是PPO的式子和流程,将原来的函数减去一项散度。这很容易让我们想到L1,L2正则这种形式,可以认为这是一项惩罚项,若两个分布差异越大,那么相同的\(J(\theta)\)下,得到的值越小。β是一个可调节的超参数,需要动态调节。

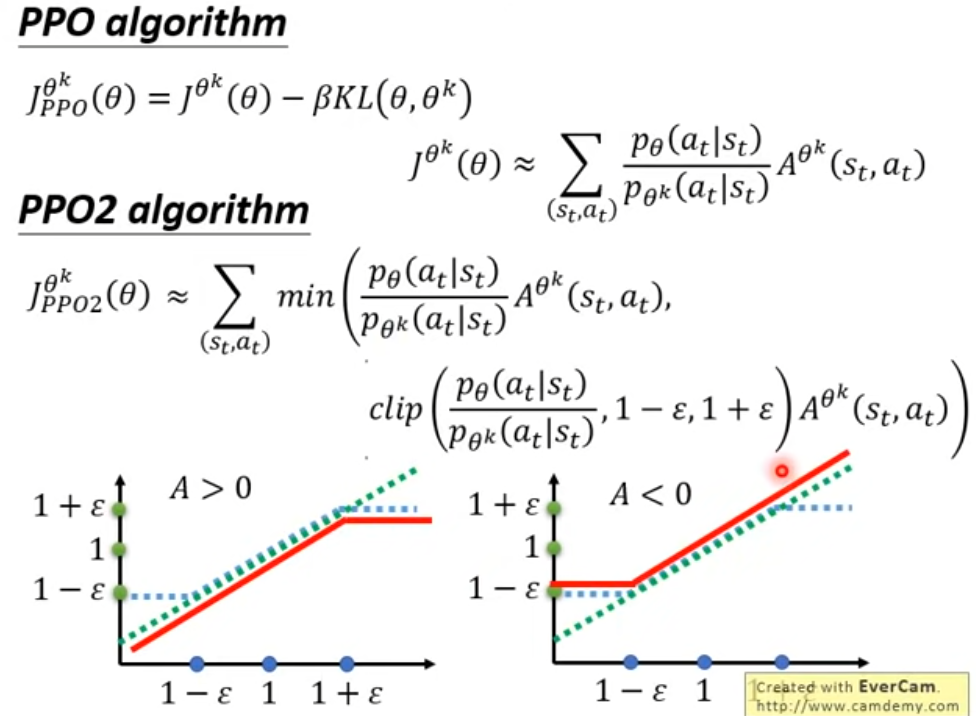
还有PPO2,将KL去除,换成一个min+clip的操作。目标和PPO1一样,让两个分布的差距不要太大。差异太大有两种比值情况,\(\frac{p_\theta}{p_{\theta^k}}\)太大或太小。当A>0时,若两个p的比值太大,那么就把值限制在clip函数中的1+ ε中,若比值过小,也会被限制在1- ε。当A<0的时候同理。