为什么需要PE?

序列信息在多种模态中都是十分重要的信息，在文字信息中，token的顺序和位置会影响句子的意思。

I do like the cat of the game , not the cat.
I do like the dog of the game , not the dog.

可以看到仅仅调换了cat和dog的位置，两句话的意思就相反。

在RNN中，会将上一个时间步的信息作为当前的输入。在CNN for seq2seq中，常使用一维卷积核来处理序列信息。

transformer使用了注意力机制，这样模型的并行度很高。然而我们观察transformer的Attention，发现本身是不具备序列信息的(若无PE作为输入)。 \[ Attention(Q,K,V) = Softmax(\frac{QK^T}{\sqrt{d_{model}} })V \] 所以需要在做Attention计算之前，通过某种方式将词序信息引入。

好的PE应满足？

首先我们可以考虑一种最简单的实现方法，使用每一个token出现的位置直接作为PE，如第一个单词赋值1，第二个单词赋值2。然而这种方法最后的值会相当的大，并且模型的外推性很差。

另一个想法稍微改进，将值定为有界的，如[0,1]，这种方法的缺点是时间步长在不同句子之间没一致的含义。

i love the cat. [0, 0.25, 0.5, 0.75, 1.00]
i love. [0, 0.5, 1.00]

上面的例子中，0.5均有出现，然而在第一个句子中代表第三个token，而在第二个句子中则代表第二个token。这是由于在不同长度的两个句子中步长不同，导致了编码不唯一。

所以理想的PE应该满足：

每一个时间步(token位置)的编码应该是唯一的。
任意两个时间步之间的距离应该在不同长度的句子保持一致。
有界，不能野蛮增长，有助于外推。
确定性，能准确计算。

PE可以分为absolute，relative，和其他。

PE的分类

大致可以分为绝对位置编码(Transformer)，相对位置编码(T5)，可训练的位置编码(Bert)，混合位置编码(ALBERT)等等。

sinusoid

absolute代表PE会与Emb直接相加，作为Attention的输入。sinusoid，也就是Transformer论文中所使用的，属于绝对位置编码。具体公式如下。 \[ PE_{pos,2i} = sin(\frac{pos}{10000^{2i/d_{model}}}) \]

\[ PE_{pos,2i+1} = cos(\frac{pos}{10000^{2i/d_{model}}}) \]

\(pos\)是单词的位置，\(i\)是dimension，\(i∈[0,256)\)。

三角函数波的频率为\(\frac{1}{10000^{2i/d_{model}}}\)，波长为\[2 \pi*{10000^{2i/d_{model}}}\]，频率随着向量维度\(i\)的增大而变小，波长是从\(2\pi\)到\(20000\pi\)的等比级数。

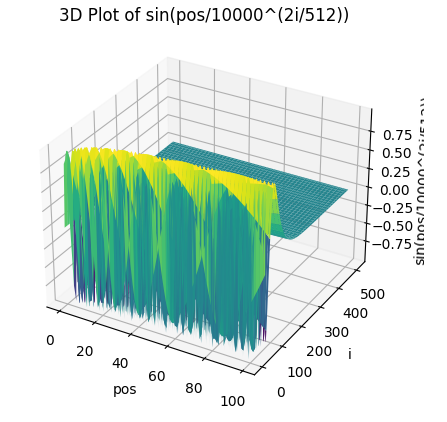
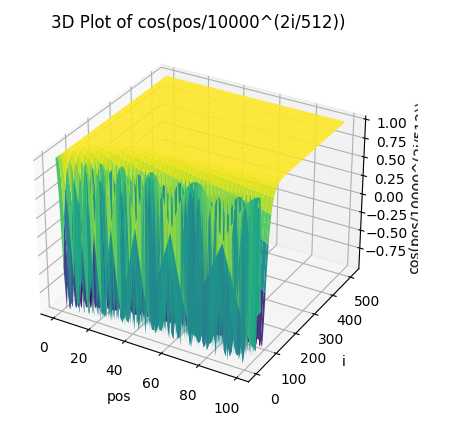
从上图看到，\(i\)越大，后续的频率就越低，波长就越长，变化就越缓。

我们固定几个pos，从中取出几个切片。

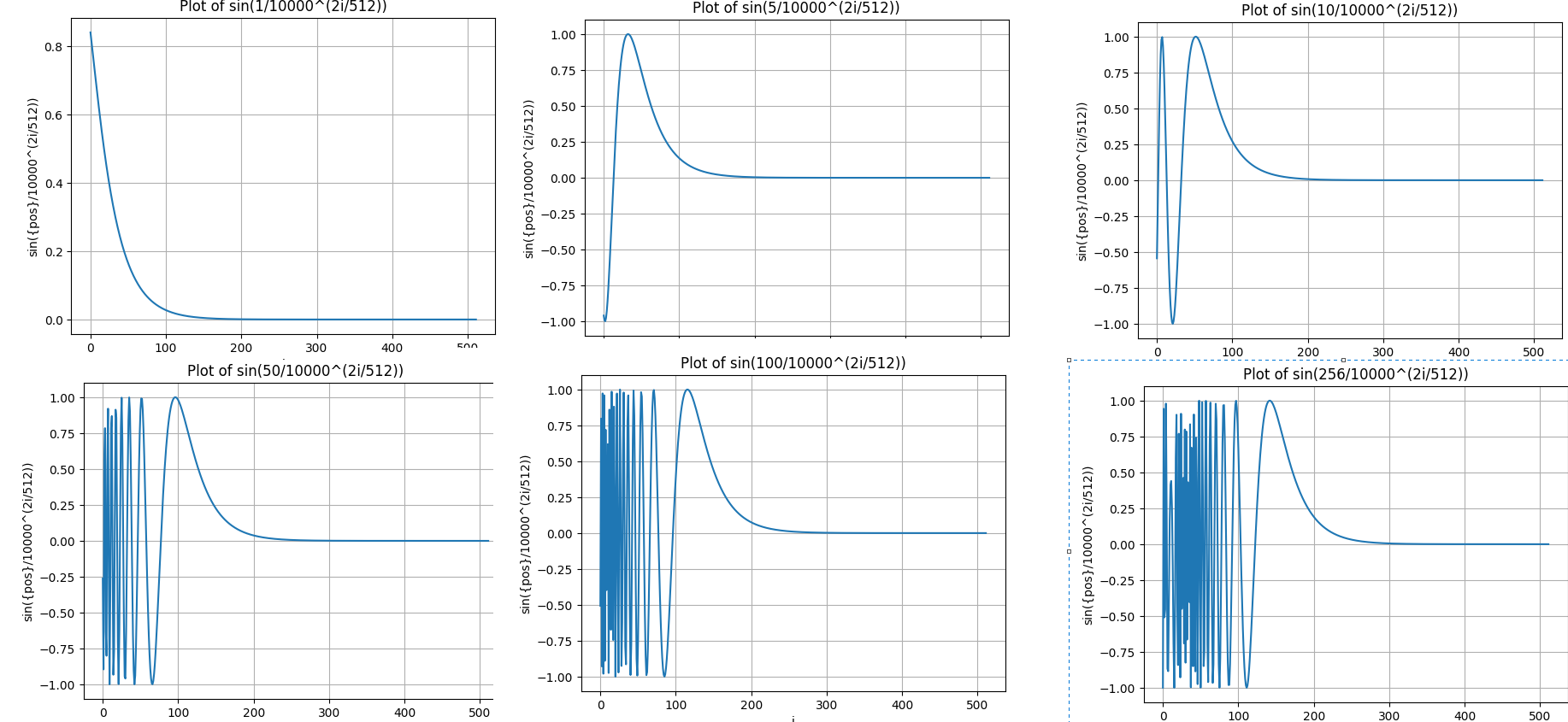
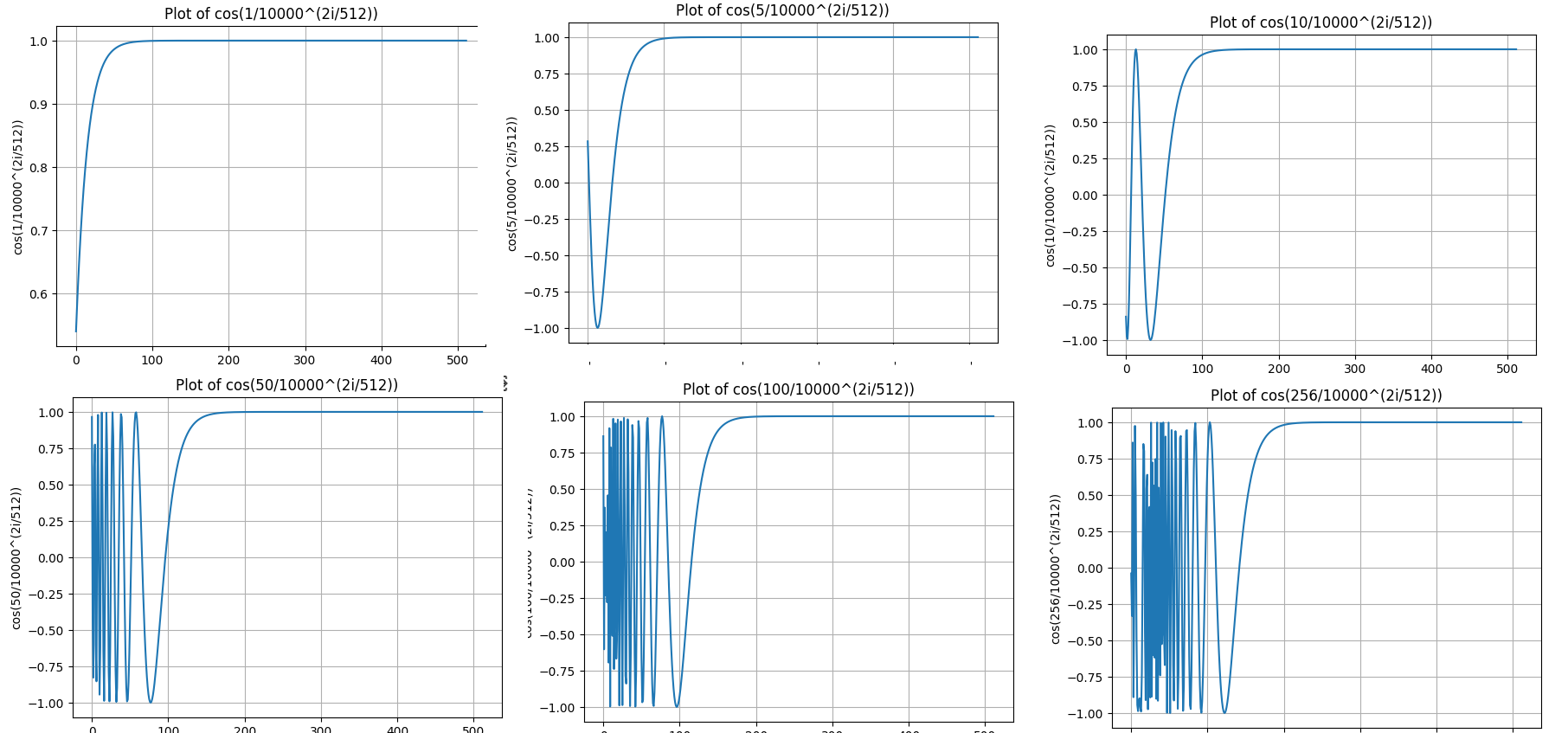
随着pos的变大，高频部分在PE中的前半部分出现的越来越多。但依然发现pos接近的PE，形状也越相似。

我们希望token之间距离越远，二者的注意力分数就越低，也就是“远程衰减”，这很符合人类的直觉。远程衰减指的是，如果向量K在向量Q的附近，那么它们的注意力分数应该偏高，反之应该偏低。根据苏神博客中推导的，sinusoid式的PE具有良好的远程衰减。

Bert式

Bert将PE直接作为可训练的参数。在具体实现中，Bert的Embedding由Word、Segment与Position三者组成，最终这三者会直接相加。

T5

待更

RoPE

待更

参考资料

[1] https://kazemnejad.com/blog/transformer_architecture_positional_encoding/ 一篇非常详实的博客。

[2] https://kexue.fm/archives/8265 苏神博客。